I've transcribed portions, book II, the Ciricle of Elements Of Analytical Geometry And Of The Differential And Integral Calculus by Davies, Charles. Published in 1866 and available on archive.org at https://archive.org/details/elementsofanalyt00davi/page/n29/mode/2up
1.The equation of a line expresses the relations which exists between the co-ordinates of every point of the line (Art.12).
2.Lines are divided into different orders, according to the degree of their equations. For example, the right line is a line of the first order, since its equation is of the first degree. The circumference of the circle is a line of the second order, its equation being of the second degree; and if the equation of a line were of the third degree, the line would be of the third order.
3.The Interpretation of an equation,consists in classing the line which the equation represents; in determining its position, its form, its limits, and the points in which it intersects the co-ordinate axes.

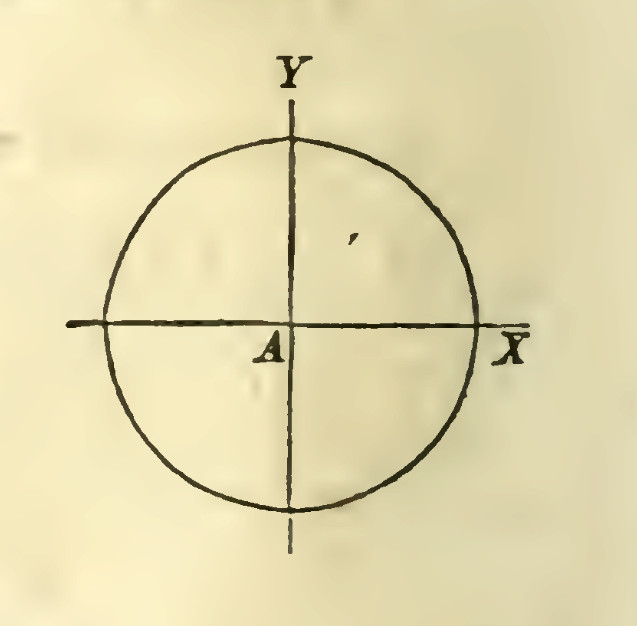
4.Let $A$ be the origin of co-ordinates, and $AX$, $AY$, the co-ordinate axis.
It is required to find the equation of a curve such, that all its points shall be at a given distance from the origin $A$. Let $R$ denote the distance, and $x$ and $y$, the co-ordinates of any point of the curve, as $P$. The square ofthe distance from the origin to any point, whose co-ordinates are $x$ and $y$, is $$ x^2+y^2 $$ hence, $$ x^2+y^2=R^2 $$ which is the equation reguired.

1. To interpret the equation, we begin by determing the points in which the circumference cuts the co-ordinate axes.
The co-ordinate of these points must satisfy, at the same time, both the equation of the circle, and the equation of the axes.
The equation of the axis $X$ (Bk. I., Art.9), being
$x$ indeterminate, and $y=0$;
if we make $y=0$, in the equation of the circle, the corresponding values of $x$ will be the abscissas of those points which are common to the circumference and the axis of $X$, that is,
$x=\pm R$;
which shows that the curve cuts the axis of the abscissas in two pionts, one on each side of the origin, and each at a distance from it equal to the radius ofthe circle.
To find the points in which the circumference cuts the axis $Y$, make $x=0$, and there results;
$y=\pm R$;
the axis of $Y$, therefore, intersects the circumference in two points, equally distant from the origin, one above the axis of $X$, and the other below it.
3. To trace the curve between these points, find the value of $y$ from the equation ofthe circle, which gives,
$y =\pm \sqrt{R^2-x^2}$.
Now, since every value of $x$, gives for $y$ two equal values, with contrary signs, it follows that the curve is symmetrical with respect to the axis of $X$; and in the same manner, it may be shown to be symmetrical with respect to the axis of $Y$.
Beginning at the point where $x=0$, we hve,
$y=\pm R$.
The values of $y$ then decreses, numerically, as $x$ increses numerically: and when $x$ becomes equal to $\pm R$, we have,
$y=0$;
hence, the curve intersects the co-ordinate axes in four pionts, at a distance from the origin, equal to $R$.
4. If $x$ becomes greater than $\pm R$, the values of $y$ become imaginary, which shows that the curve is limited both in the direction of $x$ positive, and of $x$ negative.
By placing the equation under the form,
$x=\pm \sqrt{R^2-y^2}$,
we may show, that the circumference is also limited in the direction of $y$ positive, and in the of $y$ negative.
5. By attributing a particular value to either of the variables, in the equation,
$x=\pm \sqrt{R^2-s^2}$,
the corresponding values of the other variables may be found.
If we suppose $R=1$, and then make,
| $x=0$, | we have, | $y= \pm 1$. |
| $x=\frac{1}{2}$, | gives, | $y= \pm \sqrt{\frac{3}{4}}=\frac{1}{2}\sqrt{3}$. |
| $x=\frac{3}{4}$, | gives, | $y=\pm\ \sqrt{\frac{7}{16}}=\frac{1}{4}\sqrt{7}$. |
| & etc.., | & etc.., | & etc.., |
6. If, in the equation,
$x^2+y^2=R^2$,
$x$ and $y$ denote the co-ordinates of a point within the circumference, the equality will be destroyed and $x^+y^2$, will be less than $R^2$, and we shall have,
$x^2+y^2-R^2 < 0$;
that is, negative.
For a point on the curve,
$x^2+y^2-R^2=0$;
and for a point without the curve,
$x^2+y^2-R^2>0$;
this is, positive.
7. The equation,
$y^2=R^2-x^2$,
may be put under the form,
$y^2=(R+x)(R-x)$,
in which the factors, $R+x$, and $R-x$, are two segments into which the ordinate $y$ divides the diameter; this ordinate is, therefore, a mean proportional between the two segments.(Legendre, Bk.IV. Prop.23. Cor.)
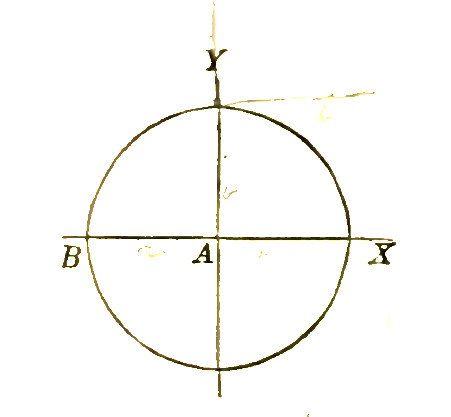
8. The equation of the circle may also be placed under another form, by transferring the origin of the co-ordinaes, from the centre to a point of the circumference.
For this transformation, we have the Formulas (Bk.I.,Art.28),
$x=a+x'$, and $y=b+y'$.
Let the origin be transferred to $B$.
The co-ordinates of this point are,
$a=-R$, and $y=y'$.
Substituting these values in the equation,
$y^2=R^2-x^2$,
we obtain,
$y'^2=wRx'-x'^2$;
or, omitting the accents,
$y^2=2Rx-x^2$;
which is the equation of the circle when the origin of co-ordnates is at the left extremity of the initial diameter.
9. When the absolute term in the equation of a line is wanting, the line will pass through the origin of co-ordinates.
For, the co-ordinates of the origin are,
$x=0$,$y=0$;
these values being substitured in any equation wanting the absolute term, will reduce both members to $0$; hence, the co-ordinates of the origin will satisy the equation of the line; and, therefore, the line will pass through the origin.
Book 2, Article 5, Page 65
There is yet a more general form under which the equation of a circle may be expressed.
The characteristic property of the circumference of a circle is, that all its points are an equal distance from the centre. To express this property, analytically, and in general manner designate the co-ordinates of the centre by $x'$ and $y'$; the co-ordinates of any point of the circumference, by $x$ and $y$, and the radius by $R$. The distance from any point, whose co-ordinates are $x', y'$, to a point whose co-ordinates are $x$ and $y$ is $$(x-x')^2+(y-y')^2=R^2$$.
This, therefore, is the most general equation of the circle referred too rectangular co-ordinates. By attributing proper values and signs to $x'$ and $y'$, the centre may be placed at any point in the plane of the co-ordinate axes.
To find the points in which the circumference intersects the axis of $X$, make $y=0$, and we have. $x=x' \pm \sqrt{R^2-y'^2}$, from which we see, that the valus of $x$ will become imaginary when $y'$ exceeds $R$, and it is plain that in that case there will be no intersection. $$ (x-x')^2+(y-y')^2=R^2\\ y=0\\ (x-x')^2+(0-y')^2=R^2\\ (x-x')^2+y'^2=R^2\\ (x-x')^2=R^2-y'^2\\ \sqrt{(x-x')^2}=\pm \sqrt{R^2-y'^2}\\ x-x'=\pm \sqrt{R^2-y'^2}\\ x=x' \pm \sqrt{R^2-y'^2} $$
To find the points in which the circumference intersects that axis of $Y$, make $x=0$, and we have, $y=y' \pm \sqrt {R^2-x'^2}$, in which the values of y will be imaginary, if $x'$ exceeds $R$.
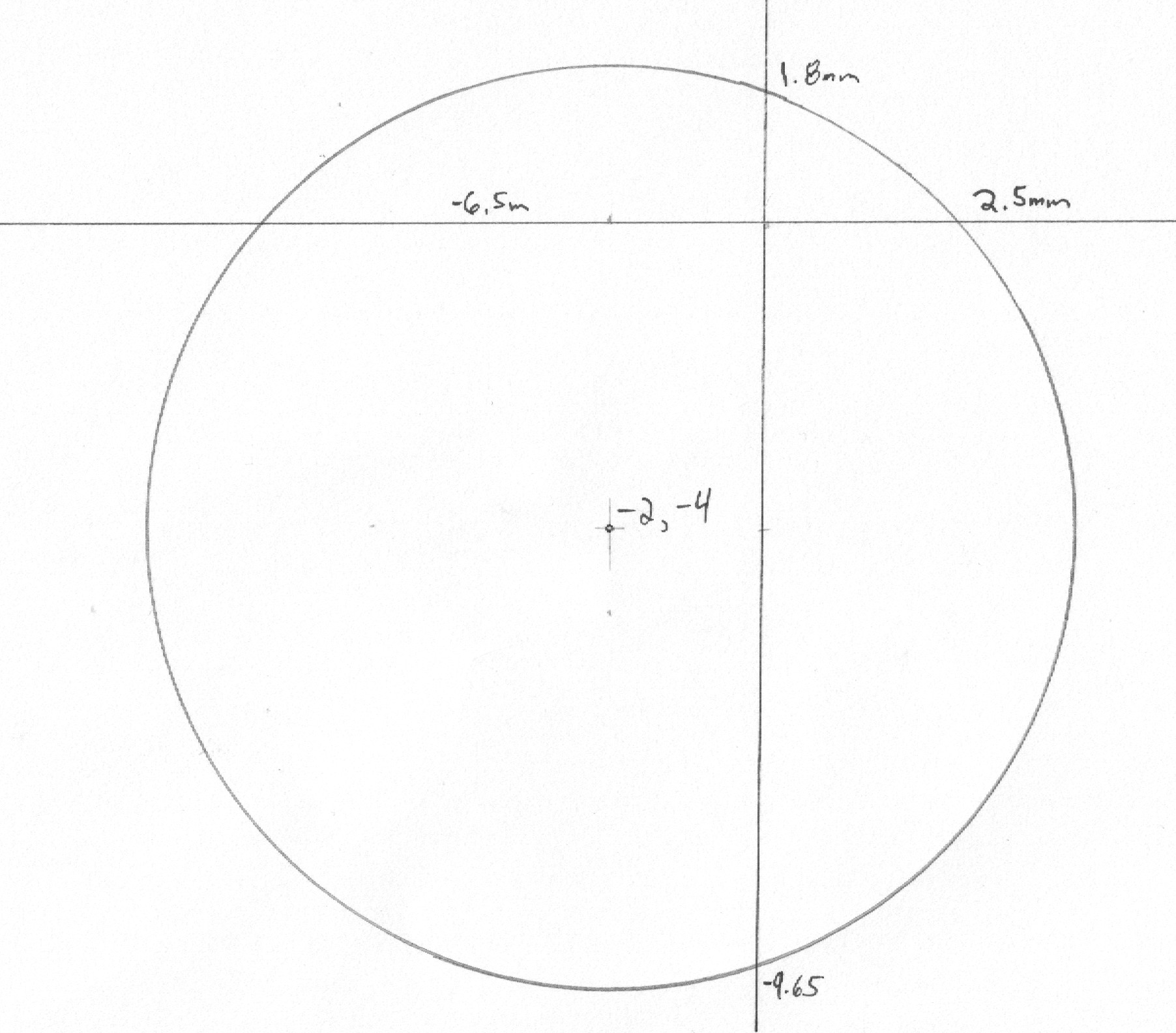
If the co-ordinates of the centre of a circle are, $x'=-2$, and $y'=-4$, and the radius equal to $6$, its equation will be, $(x+2)^2+(y+4)^2=36$, from which the circumference may be readily described. $$ \begin{align} x&=x' \pm \sqrt{R^2-y'^2}\\ &=-2 \pm \sqrt{36--4^2}\\ &=-2 \pm \sqrt{36-16}\\ &=-2 \pm \sqrt{20}\\ &=-2 \pm 4.47\\ x&=-6.47\\ x&=2.47 \end{align} $$ $$ \begin{align} y&=y' \pm \sqrt{R^2-X'^2}\\ y&=-4 \pm \sqrt{36- -2^2}\\ y&=-4 \pm \sqrt{36-4}\\ y&=-4 \pm \sqrt{32}\\ y&=-4 \pm 5.66\\ &=-9.66\\ &=1.66 \end{align} $$
Art. 6
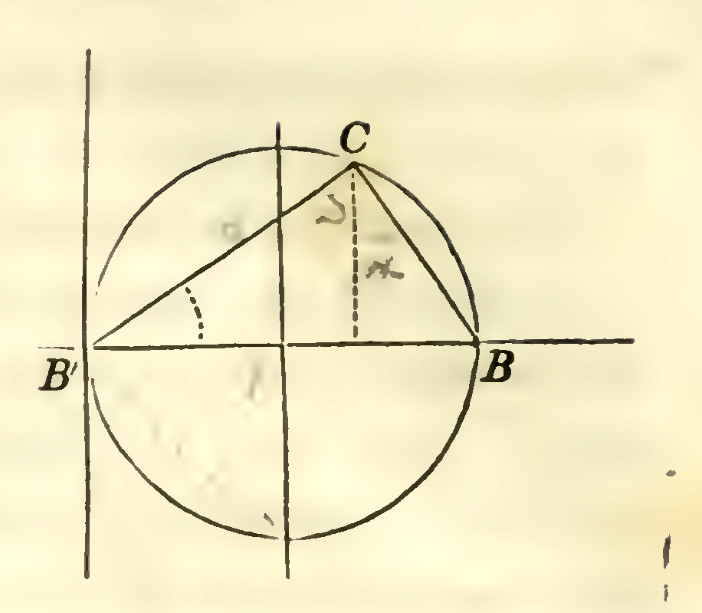
Supplementary Chords, are pairs of chords drawn through the extremities of a diameter, and intersection each other on the curve.
Art. 7
Suplementary chords of the circle are at right angles.
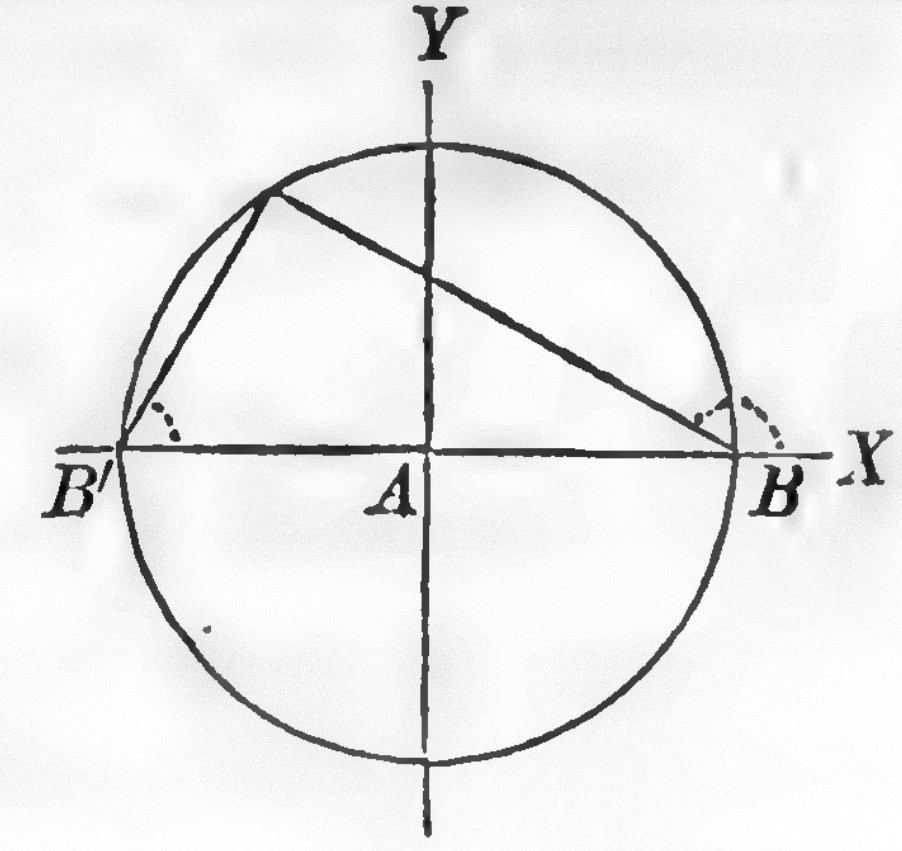
Let $A$ be the origin of co-ordinates, and $B$ and $B'$, the extremities of a diameter.
The equation of a straight line passing through a given point, is of the form $y-y'= \alpha(x-x')$.
If the line passes through the point $B$, whose co-ordinates are $x'=+R"$, and $y'=0$, its equation will be,
$$
y=\alpha(x-R)
$$
For a like reason, the equation of a straight line passing through $B'$, whose co-ordinates are $x'=-R$, and $y'=0$, is
$$
y=\alpha'(x+R)
$$
If these two lines interesect each other, the co-ordinates of their point of intersection will satisy both equations. Hence, if we suppose $x$, in one equation, to be equal to $x$ in the other, and $y$ equal to $y$, and then combine the equations by multiplying them together, member by member, the resulting equation,
$$
y^2=\alpha\alpha'(x^2-R^2)
$$
will express the conditions, that the two straight lines shall intersect on the plane of the co-ordinate axes.
But, if the point of intersection is in the circumference of the circle, $x$ and $y$ must satisy the equation,
$$
x^2+y^2=R^2
$$
or,
$$
y^2=R^2-x^2=-1(x^2-R^2)
$$
Hence, $\alpha\alpha'=-1$, or, $\alpha\alpha'+1=0$.
The two supplementary chords, therefore, are at right angles.
In the equation of the condition
$$
\alpha\alpha'+1=0
$$
the two tangents $\alpha$ and $\alpha$, are undetermined; there are, therefore, an infinite number of values which may be attributed to either of them, that will satisy the equation; hence, there is an indefinite number of supplementary chords that may be drawn through the extremities of the same diameter, each pair of which will be at right angles.
If one of the supplementary chords make a given angle with the axis of $X$, its tangent, $\alpha$ or $\alpha'$, is known; and then the value of the other tangent may be found from the equation of the condition.
If either $\alpha$ or $\alpha'$ is equal to $0$, the other will be infinite; which shows, that if one of the chords coincides with the axis of $X$, the other will be perpendicular to it.
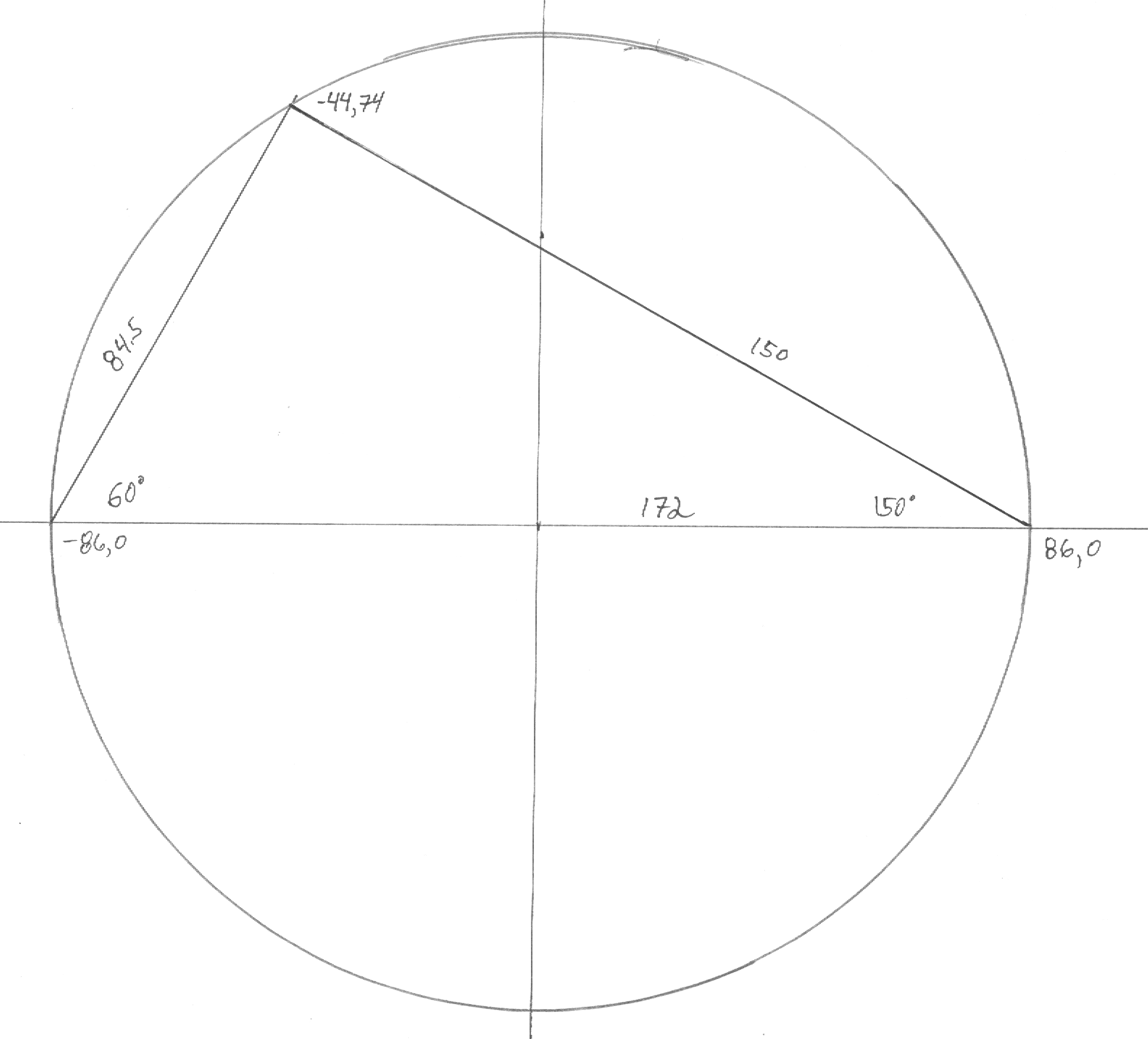
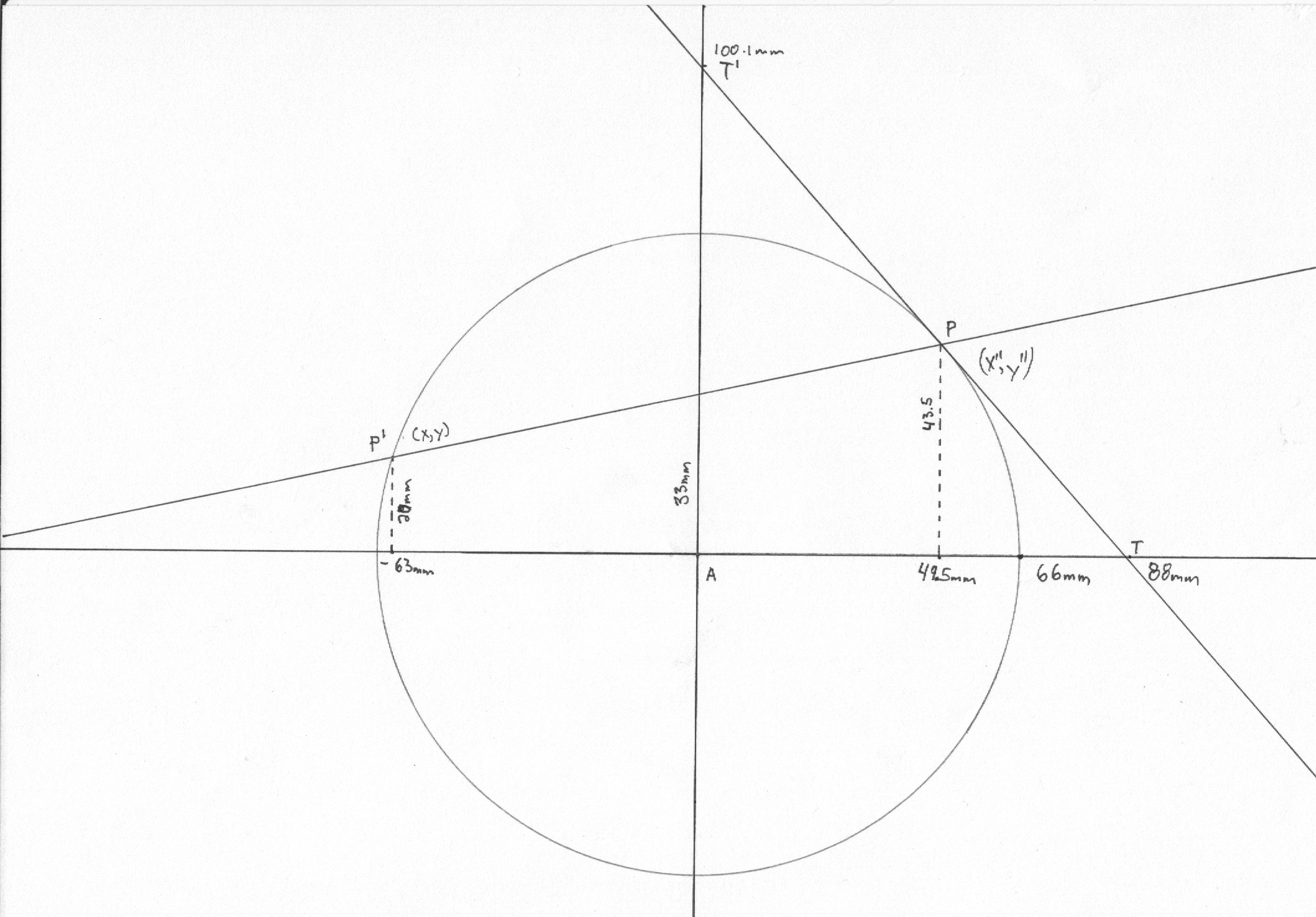
Line $B$ from point ($x=-44$, $y=74$) to point ($x'=86$, $y'=0$), 150mm
Line $B'$ from point ($x=-44$, $y=74$) to point ($x'=-86$, $y'=0$), 84.5mm
The equation of line $B$, 150mm
$$
\begin{align}
y-y'&=\alpha(x-x')\\
74-0&=\alpha(-44-86)\\
74&=\alpha(-130)\\
\frac{74}{-130}&=\alpha\\
\alpha&=-.569
\end{align}
$$
The equation of line $B'$, 84.5mm
$$
\begin{align}
y-y'&=\alpha(x-x')\\
74-0&=\alpha(-44--86)\\
74-0&=\alpha(-44+86)\\
74&=\alpha(42)\\
\frac{74}{42}&=\alpha\\
\alpha&=1.76
\end{align}
$$
Checking to see if the angles are at right angles.
$$
\alpha\alpha'+1=0\\
-.569\times1.76+1=0\\
-1+1=0
$$
Tangent line tothe circle.
Art. 8
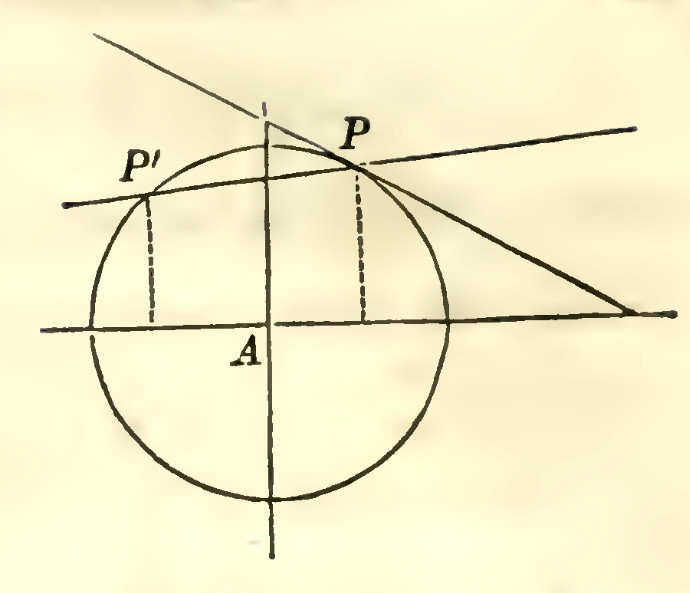
8.Two points of a curve are consecutive, when there is no point of the curve between them.
A straight line is tangent to a curve when it has two consecutive points in comomon with the curve.
To find the equation of a tangent line to a circle.
Let $A$ be the origin, and the equation of the circle,
$$
x^2+y^2=R^2, \tag{1.}
$$

Normal Line.
9.A NORMAL LINE to a curve, is a line perpendicularto a the tangent at the point of contact.
Every noraml line, in a circle, passes through the centre.
10.The tangent of the angle which the tangent line to a circle makes with teh axis of $X$(Art. 8), is
$$
a=-\frac{x''}{y''} \tag{1.}
$$
The equation of any straight line passing through the point of tangency will be of the form,
$$
y-y''=\alpha'(x-x'').
$$
The equation of condition requring this line to be perpendicular to the tangent (Bk. I.,k Art. 23-2), is,
$$
\alpha\alpha'+1=0
$$
or,
$$
\alpha'=-\frac{1}{\alpha} \tag{2.}
$$
Substiting for \alpha its value in Equation (1), we have,
$$
\alpha'=\frac{y''}{\alpha''}
$$
The equation of the normal, therefore, becomes,
$$
y-y''=\frac{y''}{x''}(x-x'')
$$
or, by reducing,
$$
yx''-y''x=0
$$
or,
$$
y=\frac{y''}{x''}x
$$
and since this equation has no absolute therm (Art. 4-9), the line passes through the origin of co-ordinates. We have thus proved a property well knowin in Elementary Geometry, viz.:that a line perpendicular to the tangent, at the point of contact, passes through the centre of the circle.
Polar Equations.
11.The polar equation of a curve, is the equation which is obtained by referring the curve to a fixed point and a given straight line. The fixed point is called the pole; the variable distance, from the pole to any point of the curve, is called the radius-vector; and the angle which the radius -vector makes with the given straight line, is called the variable angle.
Polar equation of the circle.
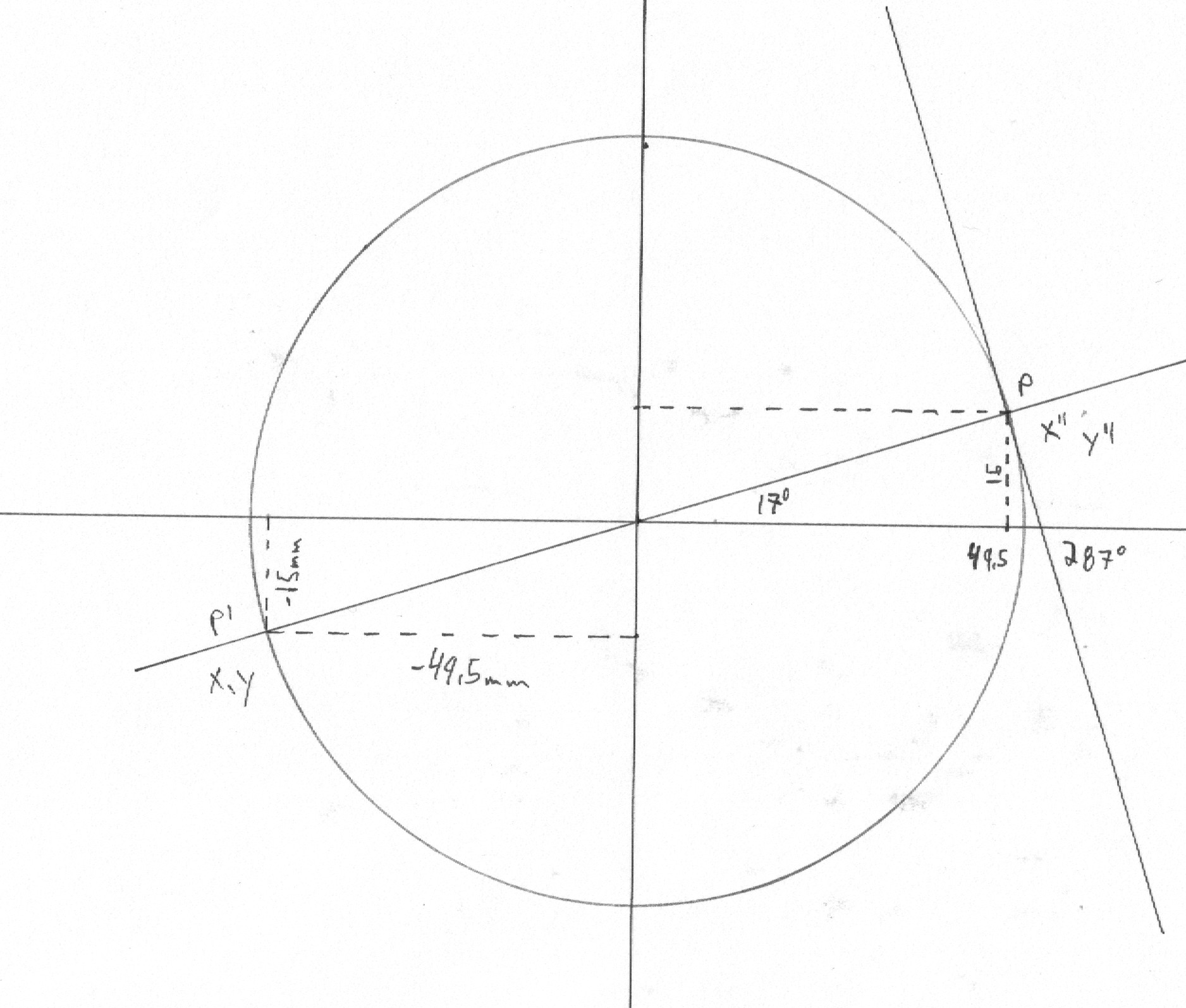
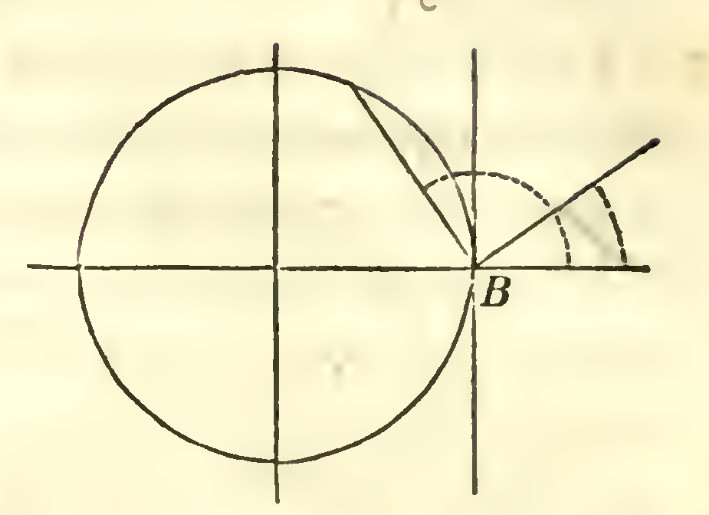
12.Let it be required to find the polar equation of the circle, when the pole is in the circumference.
The equation of the circle, referred to rectangular co-ordinates, when the origin is in the circumference, as at $B'$, (Art. 4-8), is
$$
y^2=2Rx-x^2 \tag{1.}
$$
If $B'$ is the pole of the polar co-ordinates, we have (Bk.I.,Art.36-1),
$$
x=r\cos v
$$
and
$$
y=r\sin V
$$
Substituting these values of $x$ and $y$, in Equation (1), we have,
$$
r^2\sin^2 v = 2Rr\cos v- r^2cos^2 v
$$
Transposing, and remembering that,
$$
\sin^2v+cos^2v=1
$$
we have,
$$
r^2-2Rr \cos v=0
$$
which is the polar equation of the circle when the pole is at $B'$, and the angle v, estimated from the axis of $X$.
Interpretation of the equation.
13.Since the polar equation,
$$
r^2-2Rr \cos v=0
$$
has no absolute term, one of the roots is equal to 0; which ought to be the case, since the pole is on the curve (Art.4-9).
Dividing by the value of $r$, we obtain for the other value,
$$
r=2R \cos v
$$
This value of r will be postive, when the $\cos v$ is postive; and negative, when the $\cos v$ is negative. But the negative values of the radius-vector must be rejected, since they cannot enter into the analysis (Bk.I,Art.35).
The figure also indicates the same results. For, the $\cos v$ is postive in the first and fourth qudrants; hence, the radius-vector is positive when it falls in the first or fourth angle. The $\cos v$, is negative in teh second and third quadrants; hence, the radius-vector is negative when it falls in the second or third angle.
For $v=0$, the $\cos v =1$, and we have,
$$
r=2R=B'B
$$
When $v$ increases from $0$ to $90^\circ$, the radius-vector continues positive, and determines all the points in the semi-circumference $BCB'$,
$$
B'C=B'B \cos BB'C
$$
that is,
$$
r=2 \cos v
$$
When $v$ becomes equal to $90^\circ$, $\cos v = 0$, and $r$ is $0$.The radius-vector then becomes tangent to the circumference, since the two points in which it before cut it, have united.
From $v=90^\circ$, to $v=270^\circ$, the $\cos v$ is negative; and there is not point of the curve either in the second or third angle.
From $v=270^\circ$, to $v=360^\circ$, the $\cos V$ is postive, and the radius-vector will determine all the points of the semi-circumference, below the axis of abscissas.
2. If the pole be placed at the point $B$, whose co-ordinates are,
$a=+R$, $b=0$,
the equation will become,
$$
r=-2R \cos v
$$
In this equation the radius-vector will be negative, when $\cos v$ is positive, and positive, when $\cos v$ is negative.
Hence, the radius-vector will not give points of the curve from $v=0$, to $v=90^\circ$. It will give points of the curve from $v=90^\circ$, to $v=270^\circ$; and it will again fail to determine a curve from $v=270^\circ$, to $v=360^\circ$. The figure verfies these results.
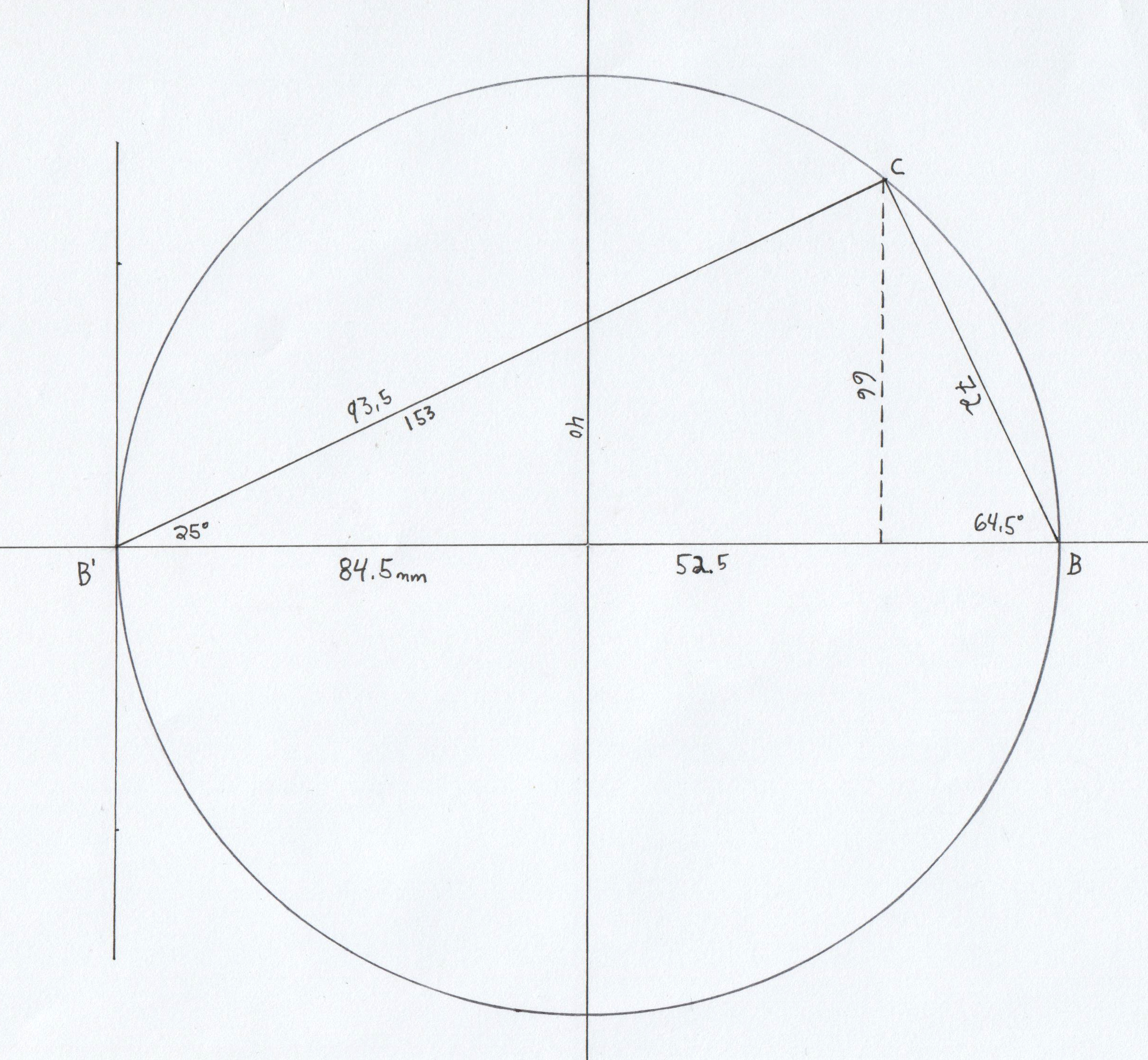
| $$ \begin{align} y&=r \sin v \\ 66&=153 \sin (25)\\ 66&=153(.42262)\\ 66&\approx 64.7 \end{align} $$ | $$ \begin{align} x&=r \cos v\\ 84.5+52.5&=153 \cos (25)\\ 137&=153(.90630)\\ 137 &\approx 138.7 \end{align} $$ |